次元(じげん)は、空間の広がりをあらわす一つの指標である。座標が導入された空間ではその自由度を変数の組の大きさとして表現することができることから、要素の数・自由度として捉えることができ、数学や計算機において要素の配列の長さを指して次元ということもある。自然科学においては、物理量の自由度として考えられる要素の度合いを言い、物理的単位の種類を記述するのに用いられる。(Wikipediaより)
なぜ、次元の話?
ちょっと難しい出だしですみません。
なぜ次元に興味を持ったかと言うと、宇宙のことや時間に興味を持ったからでした。
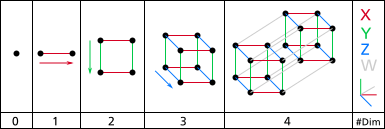
(画像はWikipediaより)
0次元とは、点のこと、点と点を結んだ線が1次元、線と線を結んだ面が2次元、面と面を繋げた立体が3次元(空間)、4次元とは…
次元について詳しく理解しているわけではありません。
本からのひらめき
なんの本に書かれていたかは、忘れましたが、次元について少しだけ理解できた概念があった。
こんな記述でした。
1次元である線と線が交わるところは、点であり0次元。
面と面が交わるところが、線である1次元。
空間と空間が交わるところが、面である2次元。
この宇宙は、3次元空間と時間が加わった4次元とされている。
もし、上で書いた理屈でいくと4次元と4次元が交わるところが、この世界である3次元です。

(画像はWikipediaより)
読書会で気付いた新たな観点
先日、読書会で面白い話を聞いた。
0次元である点は、正確には、点ではない!
・を拡大すると・
何を言いたいかと言うと、純粋な・は存在せず、よく見ると面であると言うこと、そうなると線も面であり、面は…
そんな訳で、簡易的に0次元=点と理解していたが、概念的にはある地点と考えた方がいいみたいだ。
しかし、ユーチューブで見つけた画像ですが、わたしの頭は、この9歳の子供にも追いついていない。
さて、次はどんなインスピレーションと出会えるのか。楽しみに待ってみたい。